Biochemical reactions
Biochemical reactions
Table of Contents
1. Chemical reactions and equations
[Wiki-ChR] A chemical reaction is a process that leads to the transformation of one set of chemical substances to another. Chemical equations are used to graphically illustrate chemical reactions. They consist of chemical or structural formulas of the reactants on the left and those of the products on the right. They are separated by an arrow (\(\rightarrow\)) which indicates the direction and type of the reaction; the arrow is read as the word "yields". The tip of the arrow points in the direction in which the reaction proceeds. A double arrow (\(\rightleftharpoons\)) pointing in opposite directions is used for equilibrium reactions. Equations should be balanced according to the stoichiometry, the number of atoms of each species should be the same on both sides of the equation. This is achieved by scaling the number of involved molecules (\(A\), \(B\), \(C\) and \(D\) in a schematic example below) by the appropriate integers \(a\), \(b\), \(c\) and \(d\).
An example of chemical equation:
A coefficient of \(2\) must be placed before the oxygen gas on the reactants side and before the water on the products side in order for, as per the law of conservation of mass, the quantity of each element not to change during the reaction.
2. Reaction rate
[Wiki-RR], [Wiki-RE] The reaction rate (rate of reaction) or speed of reaction for a reactant or product in a particular reaction is intuitively defined as how fast or slow a reaction takes place. The rate law or rate equation for a chemical reaction is an equation that links the reaction rate with concentrations or pressures of reactants and constant parameters (normally rate coefficients and partial reaction orders).
For a generic chemical reaction
the rate is given by
where \([\mathrm{A}]\) and \([\mathrm{B}]\) express the concentration of the reactants A and B, usually in moles per liter (molarity, \(M\)); \(x\) and \(y\) must be determined experimentally (a common mistake is assuming they represent stoichiometric coefficients, i.e. \(a\) and \(b\) but this is not the case). \(k\) is the rate coefficient or rate constant of the reaction. The value of this coefficient \(k\) depends on conditions such as temperature, ionic strength, surface area of the adsorbent, light irradiation or others.
The exponents \(x\) and \(y\) are called reaction orders and depend on the reaction mechanism. According to the law of mass action [BR2009] for elementary (single-step) reaction (i.e. for reaction with no intermediate steps in its reaction mechanism), the order in each reactant is equal to its stoichiometric coefficient (for our example if the reaction is elementary then \(x=a\) and \(y=b\)). For complex (multistep) reactions, however, as we note above, this is not true.
By using the mass balance for the system in which the reaction occurs, expressions (ordinary differential equations) for the rate of change of the concentration of the reactants and products can be derived. For our example:
3. Solver for biochemical reactions
A biochemical reaction is the transformation of one molecule into a different molecule inside a cell. Biochemical reactions are mediated by enzymes, which are biological catalysts that can alter the rate and specificity of chemical reactions inside cells.
Our solver for biochemical reactions assumes that:
- the reactions are elementary, i.e. the rate of each reaction is proportional to the product of the concentrations of its reactants
- the stoichiometric coefficients of reactants and products are 1 (e.g. \(a = b = ... = 1\)).
4. Example: Michaelis–Menten kinetics
[Wiki-MMK] In 1903, French physical chemist Victor Henri found that enzyme reactions were initiated by a bond (more generally, a binding interaction) between the enzyme and the substrate. His work was taken up by German biochemist Leonor Michaelis and Canadian physician Maud Menten, who investigated the kinetics of an enzymatic reaction mechanism, invertase, that catalyzes the hydrolysis of sucrose into glucose and fructose. In 1913, they proposed a mathematical model of the reaction. It involves an enzyme \(E\) binding to a substrate \(S\) to form a complex \(ES\), which in turn is converted into a product \(P\) and the enzyme. This may be represented schematically by chemical equations as
where \(k_f\), \(k_r\), and \(k_\mathrm{cat}\) denote the rate constants, and the double arrows between \(S\) and \(ES\) represent the fact that enzyme-substrate binding is a reversible process.
Applying the law of mass action gives a system of four non-linear ordinary differential equations (ODEs) that define the rate of change of reactants and products with time \(t\):
\(\frac{d[\mathrm{E}]}{dt} = -k_f[\mathrm{E}][\mathrm{S}] + k_r[\mathrm{ES}] + k_\mathrm{cat}[\mathrm{ES}]\)
\(\frac{d[\mathrm{S}]}{dt} = -k_f[\mathrm{E}][\mathrm{S}] + k_r[\mathrm{ES}]\)
\(\frac{d[\mathrm{ES}]}{dt} = k_f[\mathrm{E}][\mathrm{S}] - k_r[\mathrm{ES}] - k_\mathrm{cat}[\mathrm{ES}]\)
\(\frac{d[\mathrm{P}]}{dt} = k_\mathrm{cat}[\mathrm{ES}]\)
One solution of the system is shown in the figure below:
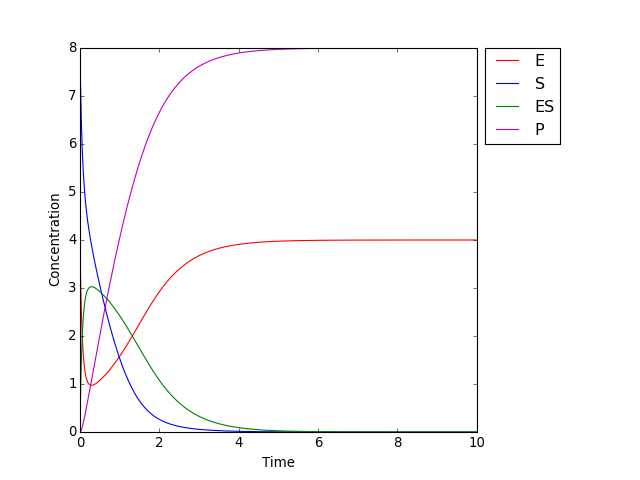
Michaelis–Menten kinetics: change in concentrations over time for enzyme E, substrate S, complex ES and product P with initial concentrations \([E]_0 = 4.0, [S]_0 = 8.0, [ES]_0 = [P]_0 = 0.0\) and rate constants \(k_f = 2.0, k_r = 1.0, k_\mathrm{cat} = 1.5\).
5. References
| [Wiki-ChR] | http://en.wikipedia.org/wiki/Chemical_reaction |
| [Wiki-RR] | http://en.wikipedia.org/wiki/Reaction_rate |
| [Wiki-RE] | http://en.wikipedia.org/wiki/Rate_equation#cite_note-3 |
| [Wiki-MMK] | http://en.wikipedia.org/wiki/Michaelis%E2%80%93Menten_kinetics |
| [BR2009] | James Keener, James Sneyd, Mathematical Physiology I: Cellular Physiology - Biochemical Reactions. Interdisciplinary Applied Mathematics, Volume 8/1 2009 |
